אוזניים, תדרים ומה שביניהם
מבוא:
הנושא שבחרנו לחקור עליו הוא ניתוח תדר תהודה. מאחר ושנינו נגנים שאוהבים מוזיקה, רצינו להבין כיצד עובדת מערכת השמיעה. גילינו שבתוך האוזן האנושית ישנן שערות שלכל שערה יש תדר תהודה ייחודי משלה אשר מגיבה הכי הרבה לתדר מסוים, וכך נוצרת מערכת שיכולה לקלוט ולזהות טווח גדול של תדרים. כאשר אנחנו שומעים צליל, האוזן שלנו מפרקת את הצליל לתדרים בודדים בעזרת השערות הייחודיות שלה, והתחלנו לחקור את נושא השמיעה בעזרת חקירת תדר התהודה. על מנת לחקור את הנושא השתמשנו בקפיצים עם משקולות – שגם להם, לכל קפיץ ומשקולת, יש תדר תהודה עצמי שונה, כמו האוזן .
מטרות המחקר ושאלות המחקר:
מטרת המחקר שלנו היא לחקור כיצד האוזן שלנו מזהה צלילים עם גוון )ספקטרום( רחב של תדרים שונים ומפרקת את התדרים המורכבים לתדרים בודדים המרכיבים את התדר המורכב שהאוזן קלטה. בכדי להגיע למטרה זו, רצינו לנסות לחקות את מערכת השמיעה שלנו על ידי שימוש בקפיצים עם משקולות שונות, מאחר ולכל קפיץ יש תדר תהודה עצמי אחר חשבנו שזה יכול לעבוד כמו השערות המיוחדות באוזן שלכל שערה יש תדר תהודה עצמי אחר חשבנו שזה יכול לעבוד כמו השערות המיוחדות באוזן שלכל שערה יש תדר תהודה עצמי אחר.
שאלות החקר:
- מהו הקשר בין המסה לבין ההיענות של המערכת וכיצד המסה של הקפיץ משפיעה על ההיענות של הקפיץ-משקולת?
- כיצד ניתן לאפיין את הדעיכה במתנד הרמוני מרוסן עם כוח מאלץ, על מנת למצוא את האמפליטודה כאשר התנועה ההרמונית דעכה?
- כיצד נוכל למצוא את התדר המאלץ בעזרת אמפליטודה של מספר קפיצים במשקלים שונים?
- כיצד ניתן למצוא את התדר של המיתר הנע בתדר קבוע בעזרת התנועה שלו?
- כיצד במערכת מרובת מיתרים נוכל לזהות את התדר המאלץ לפי היענות המיתרים השונים?
עקרונות פיזיקליים מרכזיים
תנועה מעגלית, תנועה הרמונית, מטוטלת מתמטית, תנועה הרמונית של קפיץ-משקולת, היענות קפיץ-משקול, מקדם איכות קפיץ, דעיכה של קפיץ
ניסויים מקדימים:
- השוואה בין תנועה הרמונית לתנועה מעגלית
- אפיון זמן מחזור של תנועה הרמונית במערכת קפיץ-משקולת
- תנועה הרמונית מאולצת – גרף היענות
- תנועה הרמונית מאולצת – דעיכה של קפיץ
ניסוי מרכזי:
- תדר נעלם– מציאת תדר נסתר לפי אמפליטודה
מהלך המחקר
מטרת הניסוי המרכזי היא למצוא את התדר המאלץ בעזרת האמפליטודה של מספר קפיצים בעלי משקלים שונים .
על פי הניסויים הקודמים אנו משערים שיהיה ניתן למצוא את התדר רק בעזרת האמפליטודה של המערכת בעזרת הנוסחה של גרף ההיענות: 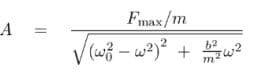
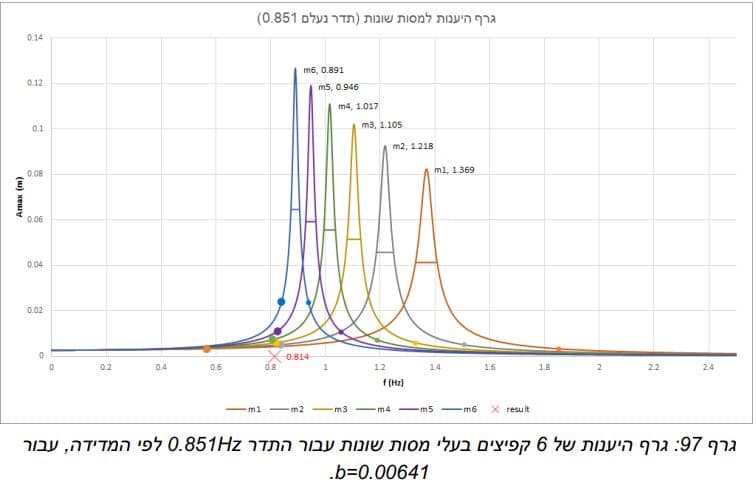
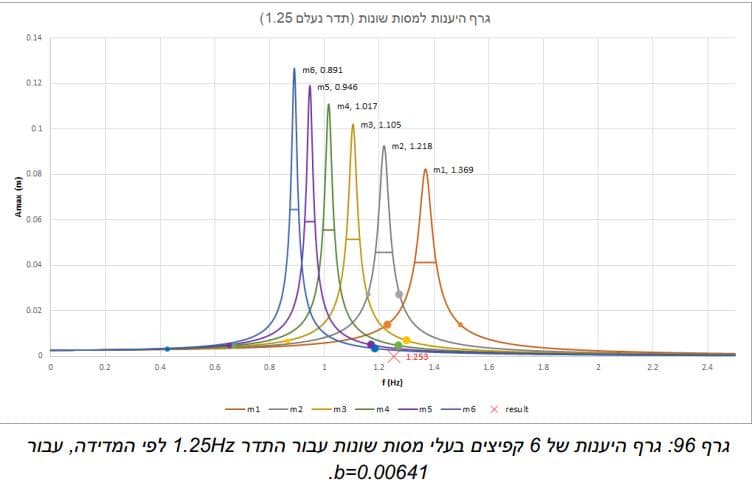
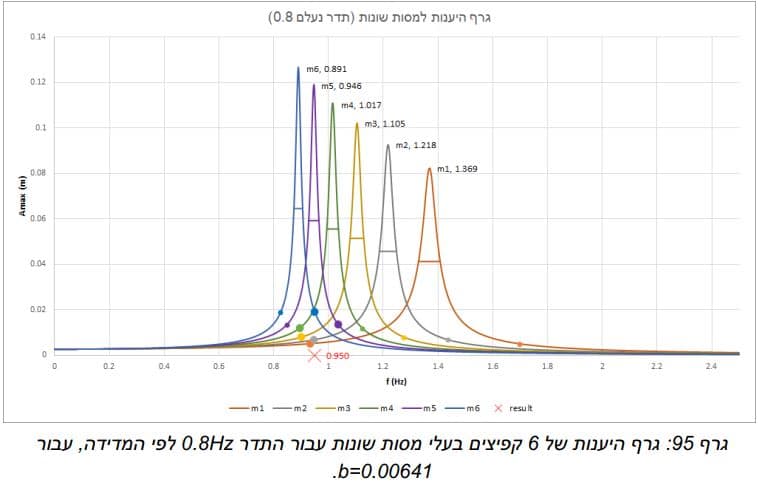
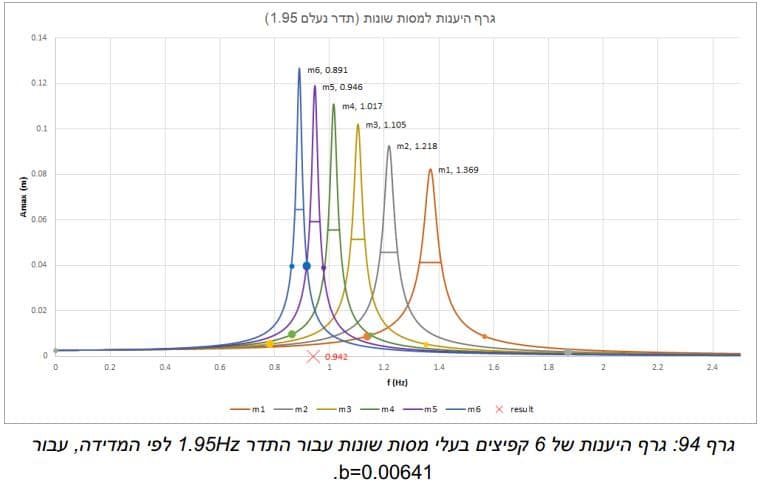
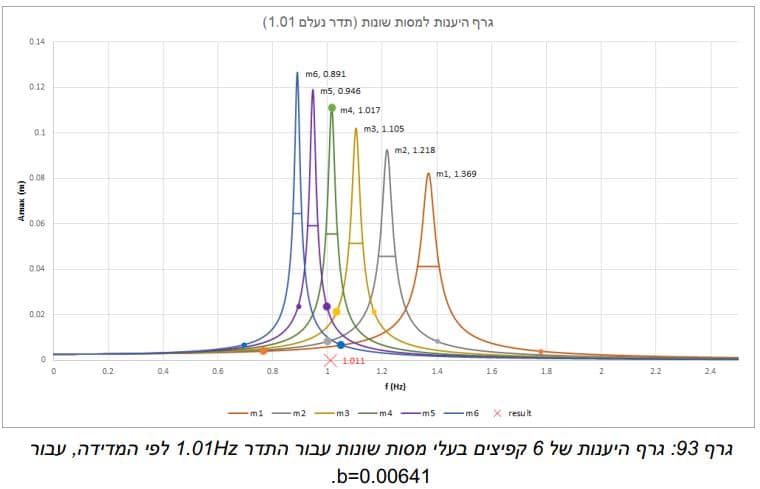
לאחר שיצרנו את הטבלה של האמפליטודה של כל מסה לפי תדר קיבלנו את הגרף הבא:
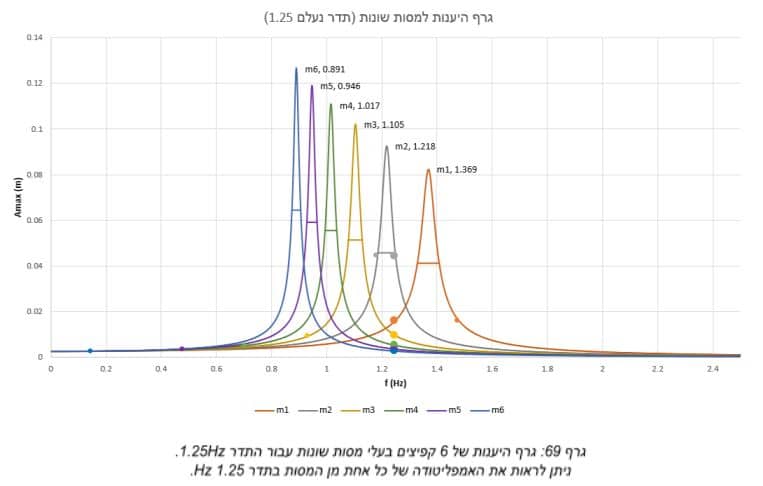
הגרף המוצג להעיל מייצג את ההיענות של המערכת קפיץ-משקולת במשקלים שונים, ניתן לראות שבתדר העצמי של כל מסה נקבל את האמפליטודה המקסימלית. נבחר תדר מאלץ מסויים אשר יגרום לאמפליטודה שונה לכל מסה. אפשר לראות לפי הגרף שאמפליטודה מסוימת מייצגת שני תדרים אפשריים לכל אחת מהמסות. כדי למצוא איזה מהתדרים הוא הנכון נמדוד איזה תדרים מתאימים לאמפליטודות שנקבל עבור משקלים שונים ונראה שרק תדר אחד יהיה משותף לכל המשקלים – זהו התדר הנעלם.
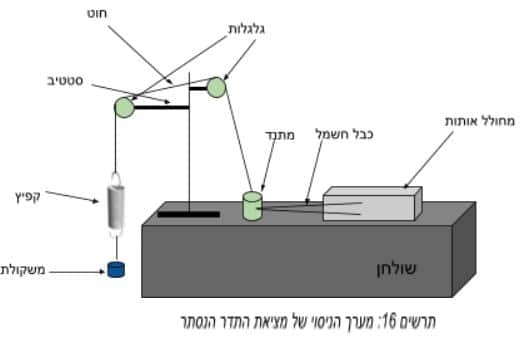
חיברנו את המערכת שתיארנו במערך הניסוי, חיברנו בכל פעם משקל אחר לקפיץ מבין חמשת המשקלים הבאים: 0.14ק"ג, 0.18ק"ג, 0.22ק"ג, 0.26ק"ג, 0.3ק"ג, 0.34ק"ג. הפעלנו את מחולל האותות בתדר אקראי ולא ידוע שלא השתנה בין משקל למשקל. הפעלנו את החיישן סונאר של PASCO ובעזרת תוכנת המחשב Pasco Capstone קיבלנו את הגרף של אמפליטודה כפונקציה של הזמן. עבור כל משקל בחרנו את האמפליטודה המקסימלית אחרי דעיכת התנועה ההרמונית. בעזרת האמפליטודה הזו של כל משקל יכולנו למצוא את התדר המאלץ. חזרנו על הניסוי חמישה פעמים לחמישה תדרים שונים.
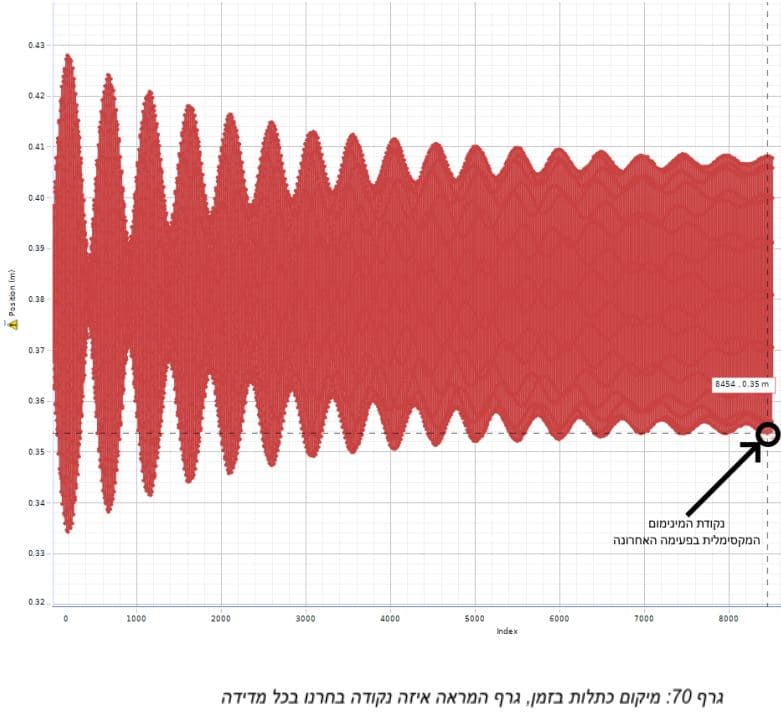
בחירת האמפליטודה המקסימלית:
חיכינו עד שהתנועה ההרמונית תדעך כמעט לגמרי, ולאחר מכן בחרנו את נקודת המינימום המקסימלית בפעימה האחרונה שמדדנו. מצאנו את נקודת האיזון של המערכת בעזרת מציאת המיקום הממוצע של כל המדידה. לאחר מכן החסרנו את המינימום שבחרנו (הנקודה המקסימלית בערך מוחלט) מנקודת האיזון של המערכת (האמפליטודה הממוצעת) וזאת האמפליטודה שהתייחסנו אליה בכל מדידה .
ממצאים:
ניתוח התוצאות:
בעזרת הנוסחא רצינו למצוא את ωכתלות באמפליטודה, אך לאחר כמה נסיונות לנתח את המשוואה הבנו שהיא מסובכת מידי. העדפנו לא להתעסק בזה אלא לבנות טבלה עם ערכים רבים מבלי לנתח את המשוואה.
יצרנו אקסל של האמפליטודה כתלות בתדר לכל אחד משש המשקלים שבחרנו להשתמש בניסוי, בהפרשים של 0.001 מ- 0 ועד-2.747.

דיון ומסקנות:
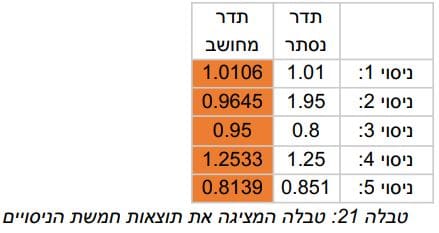
עבור ניסוי 1' 4 ו-5 קיבלנו תוצאות קרובות מאוד לתוצאות שציפינו לקבל, כפי שניתן לראות בטבלה להלן. ע בור חלק מהתדרים (0.8 ,1.95) קיבלנו תוצאות שלא תאמו את מה שציפינו לקבל. למשל, ניתן לראות שתדר 1.95 נמצא בקצה הטווח תדרים ושההיענות של הקפיצים קטנה מאוד בתדר זה. לכן קשה מאוד למדוד במדויק את האמפליטודה וכל סטייה קטנה משנה מאוד את התוצאה הסופית. עם זאת, טיעון זה איננו מסביר מדוע קיבלנו היענות גבוה עבור מסות 5 ו-6 .
אחת הסיבות שיצאו לנו סטיות במדידות הן שהתייחסנו ל Fmax כקבוע למרות שיכול להיות שהוא כן השתנה מעט בין ניסוי לניסוי (מכיוון שהוא נקבע על פי מחוגת האמפליטודה במחולל אותות, אשר ניסינו להשאיר באותו גודל אך קיים סיכוי שהוא השתנה בין ניסוי לניסוי).
עוד סיבה היא, שכאשר התדר הנסתר היה רחוק מהתדר העצמי של אחד הגרפים, האמפליטודה בגרף הייתה כל כך קטנה עד שקשה לדייק. כל טעות קטנה באמפליטודה משפיעה משמעותית בתדר. כדי להקטין את השגיאה הזו, כאשר הכנסנו את האמפליטודות לטבלה על מנת למצוא את התדר הנעלם, עשינו ממוצע משוכלל, בכדי לתת פחות חשיבות לתדרים עם הפוטנציאל לשגיאה (האמפליטודות הקטנות) ויותר משקל ככל שהאמפליטודה גבוהה יותר.
דבר נוסף שכנראה גרם לשגיאה בתוצאה זה שבחרנו שלא לנתח את המשוואה של התדר כפונקציה של האמפליטודה (כי היא היתה מסובכת מדי), אלא לבנות טבלה בעלת ערכים מאוד צפופים של התדרים. אך למרות שניסינו לעשות דגימות צפופות ככל הניתן של תדרים כדי להקטין את השגיאה, לא כל הערכים האפשריים של אמפליטודות קיימים בטבלה. לכן נאלצנו לבחור את האמפליטודה הקרובה ביותר לאמפליטודה המדודה מהטבלה ולפיה למצוא את התדר אך זה כנראה לא היה מספיק מדוייק.
עוד סיבה היא שבחלק מהניסויים לא חיכינו מספיק זמן כדי שהתנועה ההרמונית תדעך עד הסוף. ולכן כאשר לקחנו את האמפליטודה המקסימלית, היא ככל הנראה לא היתה מדויקת כי היא נלקחה מרגע שבו עוד הייתה דעיכה.
בנוסף בכל הניסויים התייחסנו לכל המסות בין הניסויים ולקבוע קפיץ כשווים בכל המדידות. אך בעצם המסה השתנתה במעט בין מדידה למדידה ויש סיכוי גדול שמכיוון שהשתמשנו הרבה באותו הקפיץ גם קבוע הקפיץ השתנה במעט, דבר זה יכול גם הוא להביא לסטייה תוצאות הניסוי.
גם לפי תוצאות של האמפליטודות שחושבו לפי הדעיכה היו אי דיוקים. הם נובעים בעיקר בגלל שכאשר נותנים לאקסל לחפש את נקודות המקסימום בפעימה, הוא לפעמים מוצא נקודות גדולות מדי בגלל "רעש" במדידה. בעין אפשר לראות את זה לפעמים, אבל האקסל לא יודע להוריד את הרעשים האלה בצורה יעילה תמיד.
מעניין לראות שעם כל הטעויות הללו, היה אפשר בכל זאת להגיע לתוצאות די קרובות לתדר המקורי, גם אם לא היינו בדיוק על התדר העצמי של אחד מהקפיצים.


